Numeroso: Numbers come alive in this fast paced game, that's easy to learn, and fun to master!

Numeroso is a great game for the whole family, because it’s easy to learn in a minute, yet interesting enough to bring you back for rematch after rematch. It’s a casual game, but its depth will surprise you!

The Origin Story

This fall, game designer Federico aimed to create an easy yet engaging game to enjoy with his young daughter and her cousins. He envisioned a simple card game where players match factors and primes to be the first to get rid of their cards.

During a family dinner in November, Federico introduced the game, "Numeroso," to the children. They quickly grasped the rules and were engrossed, playing numerous rounds before and after dinner. The game's appeal was evident as the children eagerly requested to play again during their next gathering, inspiring Federico to share Numeroso with a broader audience.

Why so Easy to Play?

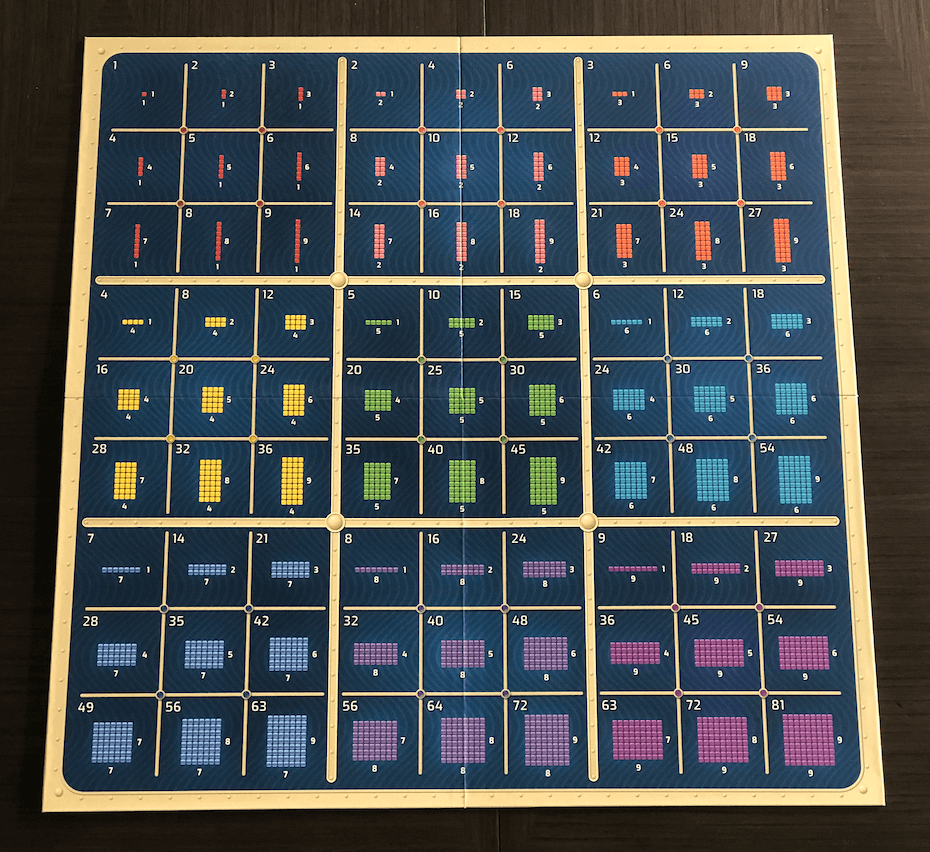
The game is so easy to play, in part, thanks to the way the Numeroso Cards represent the prime factorization both visually and numerically. Allowing players to quickly determine which cards have a common factor and which cards are prime, identifying matching cards to play on their turn.

Players can easily identify if the two numbers have common factors by looking at the prime factorization. For example here, both 36 and 42 have 3 and 2 as prime factors. You can also see visually that they both have yellow triangles (groups of 3) and blue line segments (groups of 2).

See the 3 groups of 3 groups of 2 groups of 2 dots?

Here there’s 7 groups of 3 groups of 2 dots.

Numeroso Features

• Players: 2-6+

• Ages: 7+

• Average Duration: 5 minutes

• Deck Setup: 1 deck for 2-4 players, or 2+ decks for 4-6+ players

• Objective: The aim is to get rid of your cards as quickly as possible by playing cards with matching factors with the previously played card, or by matching primes with primes.

• Numeroso cards make it easy to play the game with just a basic understanding of number

Learn to Play in 1 Minute!

The game takes a minute to learn, and we have the video to prove it…

Simple Rules, Rich Strategy

Even though the game has simple rules, there's a rich strategy to explore that will bring you back again and again.

Astute players can infer their opponents' cards and strategically play unmatched cards, compelling opponents to draw a card and forfeit their turn!

For example, if you suspect your opponent is out of multiples of two, play an 8. Since its only made up of twos (2x2x2), your opponent would have to draw a card (assuming they in fact don’t have a multiple of 2).

Downloadable Rules

You can download and print the rules, which include an optional set of rule extensions that add the ability to skip players, reverse the order of players, and force players to draw cards.

We recommend everyone starts with the simple rules, and only try the extended rules if it’s appealing after playing a few rounds.

Where to get Numeroso?

Follow one of the links below to get yourself a copy of Numeroso today!

Difference Squares: A Magical Mathematical Sandbox

Mathematics can seem magical sometimes, intricate patterns can emerge from following simple rules in surprising ways. Like all good magic, it begs to be explained, which provides a very effective way to cultivate intrinsic motivation to do mathematics.

This is one of our all-time favorite math activities to explore. It goes by many names Diffy, “Difference Squares,” or you may have seen it at a Julia Robinson Math Festival where its called the “Difference Engine.” 

We’ve led explorations on this topic with people of all ages, 5-65+. As a teacher, it’s the kind of activity that you can come back to time and time again and learn something new each time you explore. 

Embrace the unknown, model taking risks, and NOT knowing it all!

For most, it may seem scary, the idea of exploring a mathematical context with your students when you may not know all the answers to the questions that may arise. This is normal. In fact, the flip side of that is, if your students never see you interact with mathematics that you aren’t totally sure about, they develop the false notion that mathematics is all about procedures and right answers. 

What’s special about this activity? 

• Open Middle, and potentially open beginning and ending as well! “Choose your own Adventure”

• Easy to differentiate for pre-k through college-level mathematics (one person is doing single-digit subtraction, while another may be coding or using algebra)

• Provides an authentic mathematical context that motivates all 8 mathematical practices

• Connects to *active research in mathematics

Lesson Overview:

1. Play Difference Squares with dice

2. Notice/Wonder about the results of their games

3. Play Difference Squares by choosing the numbers, or explore another research question

4. Extension: Code a Difference Square Bot on Scratch

Over the years we have introduced the context in a variety of ways, our favorite being as a game.

Game Launch

If you haven’t noticed yet, we love using games in math class. The benefits of launching this exploration as a game include...

• Games are “branded” as fun

• With games, taking risks and making mistakes are naturally part of the learning process

• Can make doing something repeatedly seem effortless or even fun

• Generate lots of examples that serve as the basis for exploring patterns, analyzing and modeling data

How to Play the “Game”

1. Roll dice four times and record each number on a corner of a square

2. For each pair of corners that are next to each other, find the difference between the two numbers (positive difference, AKA absolute value of the difference) and write it at the midpoint between the two numbers

3. Draw a line connecting each of the differences to make a tilted square inside the original square.

4. Repeat step 2 with the most recent set of 4 numbers

5. Continue until you reach all zeros (if you don’t want to give it away that it always goes to zeros you could phrase this as continue until you get the same 4 numbers twice in a row)

6. Whoever has the most number of squares wins (You could say players get 1 point for each square that’s filled out)

We made a Jamboard that has two different kinds of Difference Square Templates. Click below and then click on the three dots in the top right and make your own copy to edit as you see fit.

Differentiation 

• For younger students, new to finding differences/subtraction, you can have students build the numbers with connector cubes and place the number of cubes next to each other to visually/physically find the difference.

• Adjust the range of numbers they can “roll” using random number generators with different ranges, such as four-sided, ten-sided, or twenty-sided dice, or make a spinner use a digital random number generator.

Notice and Wonder

Once students have had enough time to play at least 3 or 4 rounds, you can bring the group together to discuss what they notice and wonder. 

Potential Notice and Wonder

• It always goes to zero

• Right before it hits zero, all the numbers are the same

• If you see 0,N,0,N, you are only two steps away from all zeros

• Does it really always go to zero?

• What starting number had the most number of steps to get to all zeros?

• Wonder what would happen if we used a triangle or pentagon to start instead?

• Wonder what would happen if we used fractions, decimals, or other kinds of numbers?

• Wonder what would happen if we did something else with the numbers instead of finding the difference?

A Garden of Forking Paths

This is where the path forks, depending on which rabbit hole and how deep you want to go. Let students work on a question that interests them, and if they’d like they can work with others with similar interests.

While it’s tempting to explore some of the variations like what happens if you use triangles or pentagons, or change the rules, I would hold off till you squeeze more juice out of the original context. Sometimes keeping the parameters tighter leads to more interesting discoveries.

We will elaborate on a few paths that we’ve found fruitful. However, you know your students best, so we can’t tell you exactly which path to take. 

Potential Questions to Explore

• If you choose the numbers, can you find a set of starting numbers that makes a chain of more than 10 stages before it gets to all zeros?

• What’s the longest chain you can create?

• What’s the longest chain you can create with just zeros and ones?

• How many different ways can you begin with just zeros and ones? 

• Will you ever get a number other than 0 or 1 as the difference if you start with just zeros and ones? 

• Can you make a flowchart that shows all possible paths to four zeros?

• What’s the longest chain you can create with zeros, ones and twos?

• What’s the longest chain you can create with numbers between 0-10, 0-100, 0-1000?

A Note on Choosing “ANY” Number?

At this stage you can have students play the game again, but now they can choose ANY number they want! 

What does ANY number mean? 

I’d suggest sticking to positive whole numbers at first.

Some students will naturally stick to nice numbers, say under 100, multiples of 10, etc. Other students will immediately jump to the biggest number they can think about or write down. Of course, those students will have to find the difference between those huge numbers, and will quickly realize that even those big numbers still drop down to zero quite fast. 

Expanding the Meaning of Any Number and the Tools Allowed

When it feels right, if students want to add negative numbers or fractions and decimals, go for it! Maybe this is the right time to introduce a new concept or skill, maybe not. 

Don’t be afraid to pull out tools like calculators, spreadsheets, or even using this as a motivation to code. This does not diminish the mathematical experience here, and in many cases can really enrich the students’ experience.

In fact, the last few times we’ve explored this with students we’ve used Scratch to code a Difference Square Bot that can run the numbers for us!

Computer Science Extensions

Level 1: Write a program in Scratch that asks the user for the four starting numbers and spits out the differences at each stage until it hits all four zeros, recording how many stages it takes to reach all zeros.

Level 2: Write a program that, given a range of starting integers between 0 and N, will try every possible set of four starting numbers, and record which set generates the longest chain.

Tip: Start With Pseudocode

I always like to start with having the students write some pseudocode, and then collecting ideas into a draft to help hone the programming work.

Extension Questions

• What happens when you use fractions, decimals, or irrational numbers?

• What happens to the length of your chain if you double all the starting numbers? What about multiplying all the starting numbers by a number N?

• What can you say about a set of four numbers that wouldn’t ever reach all zeros? In other words, what would have to be true about the sequence of numbers in a difference square that never reaches zeros?

• Can you find such a set of four numbers that would never reach all zeros? (If you give up, and want to see the solution, the best explanation we’ve found is from Dan Finkel of Math For Love, check it out HERE.)

*Active Research: Clausing, Achim (2018). "Ducci matrices". American Mathematical Monthly. 125(10): 901–921.

MULTI Home Guide

Let Joy Be Your Guide!

What do you notice? What do you wonder?

This is a guide for parents and caregivers who want to help players discover the underlying mathematical structure behind the MULTI™ board game.

First off, we think it’s important to say, it is perfectly fine to just play MULTI, with no other goal than to have fun!

In fact, if you let joy be your guide, you will undoubtedly be doing mathematics, plain and simple.

That said, we wanted to dive a bit into some topics that are likely to arise and questions that can help draw out the mathematics naturally embedded in the game. 

The set of questions below are designed to be easy to begin to explore, with enough depth to challenge even the most veteran mathemagicians amongst us. 

The structure of multiples and factors are front and center in this game! However, depending on the player’s familiarity with numbers, the structure may be hidden at first, like a map hidden in plain sight.

If you’d like to dive deeper into mathematics you can start by focusing on any of the following questions, based on interest and familiarity with the concepts.

These questions are meant to be conversation starters, and the answers I include are by no means comprehensive.

Spoiler Alert: We have included some possible answers to each question. If you want to explore a question without any clues, just ignore the italics text under the questions.

Here’s a list of the key topics that could come up for players in different age ranges.

Key Topics

EARLY ELEMENTARY (K-2)

• Arrays, rectangles, area, square units, etc.

• Square Numbers

• Recognizing patterns and structure

• Symmetry

• Strategy in general, openings and endgame situations

UPPER ELEMENTARY (3-5)

• Arrays, rectangles, area, square units, etc.

• Square Numbers

• Recognizing patterns and structure

• Symmetry

• Strategy in general, openings and endgame situations

• Multiples, common multiples

• Factors, common factors

MIDDLE SCHOOL AND BEYOND

• Arrays, rectangles, area, square units, etc.

• Recognizing patterns and structure

• Symmetry

• Strategy in general, openings and endgame situations

• Multiples, common multiples

• Factors, common factors

• Combinatorics

• Game Theory

• Computer Science, coding, machine learning, etc.

---

Patterns on the MULTI Board

Single, Double, Triple, & Quadruple Plays, Oh My!

Which numbers come up the most? Which numbers come up the least? Why?

There are single, double, triple, and quadruple plays. For example 1, 25 and 81 only come up once, and 12, 18, and 24 come up four times! In the picture on the right, you can see how 18 is a quadruple play. The numbers that come up four times have two different pairs of factors(on the factor board), for example 18 is 2x9, 9x2, 3x6, and 6x3, showing up in the two’s, three’s, six’s, and nine’s mini boards.

Can you find all the quadruple plays?

Try placing black Xs on all the quadruple plays, red Xs on the triple plays, white Os on the double plays, and green Os on the single plays.

What are some of the best quadruple plays? Why?

Answers will vary depending on the situation, playing style, and preference.

Multiple Symmetry

The 4th multiple in each mini tic tac toe board mirrors the location of multiples of 4 on the big board.

Where are the multiples of 4?

The multiples of 4 are in the middle row on the far left of the entire MULTI board, but also in the same spot on each of the mini tic tac toe boards. This pattern is highlighted in the picture to the right. There are a few extra multiples of 4, can you find them?

Why does this pattern exist?

These patterns exist because each multiple of 4 is the 4th multiple of another number, and therefore would be on the left of the middle row.

What multiples are in the centerboard? Where else are those numbers?

Multiples of 5, they are in the center of each mini board as well.

Where are the square numbers? How many times do each of them show up?

The square numbers are found at 1x1, 2x2, 3x3, 4x4, 5x5, which gives you the 1st number in the One’s Board, and the 2nd number in the Two’s board, 3rd number in the Three’s Board, etc. The numbers 1, 25, 49, 64, and 81 are single plays, while 4, 9, 16, and 36 are triple plays.

What Moves are possible in this turn?

Sometimes players may get stuck, and aren’t sure what to move. Its useful to narrow down what to consider, by thinking about what moves are possible. For example if the tokens are on 4 and 7, you only need to consider multiples of 4 and multiples of 7, that have not yet been claimed. At the beginning of the game, that may be 7 x(1,2,3,5,6,7,8, and 9) and 4x (1,2,3,4,5,6,8,9), and at the end of the game there may only be a few options.

---

Strategy Talk

What are the best opening moves? What should you consider?

Answers will vary, but arguments can be made for quadruple plays on the basis of quantity, and an argument can be made for certain locations being more quality moves to start.

How can playing on a square number guarantee you can play on the same MINI Tic Tac Toe board on your next turn? Does it always work?

The Power of Playing on Square Numbers

If you have both tokens on the same number on the Factor Board, then your opponent can only move one off during their turn, leaving you with another possible move with that factor. However, playing square numbers doesn’t always work this way, for example if you play on 36, but you use 9x4 to get it.

How can you prevent a player from getting a square they need for tic tac toe? 

There are two main ways to block a player from getting a square they need. The straight forward way is to take the square yourself. However, another way to do it is to avoid placing a token on the factors they need to make the number they need for tic tac toe. For example, say they need to get 15, you would avoid having a token on either 3 or 5, since you can only get 15 by doing 3 x 5. 

What are the most important squares/locations?

Answers will vary depending on the situation, playing style, and preference.

ENDGAME

Who has a path to win? What moves are possible?

How far back do you have to go to find a pathway to a different winner?

Take a picture of the game a few steps before the end, and see if you can find an alternate ending to the game.

Who has a path to win?

What moves are possible?

Can either X or O guarantee a win?

Can the game end in a simultaneous win?

We like to call this a true “win-win!”

---

Challenge Questions

These questions are a bit more involved, and can lead you down some fantastic mathematical rabbit holes involving combinatorics, game theory, and computer science. We’d love to hear from anybody who’s gone down one of these rabbit holes, and learn about what you discovered.

How many different games are there?

How many different game states are there?

What’s the best strategy?

How could you write a program to play the game?

---

Spark More Joyful Mathematics!

If you made it this far you’ve probably enjoyed MULTI a bunch by now. Please share about the game with friends and family and help us spark joyful math moments in more homes!

MULTI is available now in our shop and on Amazon!

MULTI Lesson Plan

How to Use this Lesson

This is meant as a general outline for how to structure a lesson around MULTI. Whether your students are in early elementary, upper elementary, middle school or above, this structure will work to help groups of students pull out the many mathematical concepts connected to playing MULTI. The lesson is also easy to adapt to various in-person or distance learning settings.

Instead of writing a lesson for each grade band such as K-2, another for 3-5, and another for middle school and beyond, I will describe the mathematics each grade band could potentially get into and leave it to the teacher to decide what concepts to guide their students through.

Also, the lesson plan could be implemented (without the second game) in about 50-60 minutes, extended to a 90 minute block periods, broken up into several sessions or even repeated to dig deeper into a topic.

If you have any questions about how to weave specific topics into a lesson or how to adapt the lesson to your setting, don’t hesitate to contact us.

Key Topics

Early Elementary (K-2)

• Arrays, rectangles, area, square units, etc.

• Square Numbers

• Recognizing patterns and structure

• Symmetry

• Strategy in general, and/or for openings and endgame situations

Upper Elementary (3-5)

• Arrays, rectangles, area, square units, etc.

• Square Numbers

• Recognizing patterns and structure

• Symmetry

• Strategy in general, and/or for openings and endgame situations

• Multiples, common multiples

• Factors, common factors

Middle School and Beyond

• Arrays, rectangles, area, square units, etc.

• Recognizing patterns and structure

• Symmetry

• Strategy in general, and/or for openings and endgame situations

• Multiples, common multiples

• Factors, common factors

• Combinatorics

• Game Theory

• Computer Science, coding, machine learning, etc.

Lesson Plan

What do you notice?

What do you wonder?

Notice/Wonder (5-15 minutes)

• Display the Factor Board, MULTI board, or both to your students. (Depending on your setting, you could also have each student holding a print and play board or pairs of students in front of each board.)

• Ask “What do you notice?” and “What do you wonder?”

• Consider using a “Think, Pair, Share” model to help generate and record a greater number of student observations.

• Record Notice and Wonder on the board, document, or chart paper.

Review the Rules

Teacher-led or in small groups/partners

The Game Reveal (5-15 minutes)

• “This is a game called MULTI, here are the rules…”

• This could be teacher-led guided reading using a slideshow, or you could just hand out the rules and let them figure it out, or somewhere in between.

Play Time (20-30 minutes)

• Give students at least enough time to finish one game which typically can last between 15-30 minutes. If students finish a game earlier than others, have them play again.

• Once every pair has completed a game, you can ask everyone to pause and take a moment to think about what they noticed/wonder about the game now and/or what strategies did they and their partner use? 

Strategy Talk

What’s the best strategy here? How do you know?

Sharing Strategies (10-20 minutes)

• If possible, have students switch partners and share the strategies they used. 

• Next, have students share out their strategies with the whole group.

• Record their strategies in the board, document or chart paper.

Reflection (5 minutes) 

• Ask students to consider the strategies shared when deciding how to play in the next game.

• You could have students record and/or discuss with a partner a strategy they might try in the next game.

Play Again (20-30 minutes)

• If time permits, have students play again using what they learned in the first game and strategy talk.

• Switch partners if desired/possible.

Exit Ticket (5 minutes)

There are lots of possible exit tickets depending on the topics discussed in the lesson. Here are a few examples...

• Describe a pattern you noticed on the MULTI board.

• Where on the board do you find the multiples of 5? What about the multiples of 9?

• What number comes up the most?

• What numbers come up the least?

• What’s a good opening move?

• Describe your strategy.

• Describe strategy your opponent used against you.

• Show students an endgame situation and ask them to describe what they would do and why?

• Show students a game situation and ask them to decide who they think will win and why?

• How many different possible games are there?

Where can I get a copy of MULTI?

You can purchase the digital print and play version and table top edition in the Joyful Mathematics Shop, the table top edition is also available on Amazon.

Available now in our shop and at Amazon!

Fun With Collatz Conjecture: How an Unsolved Problem Provides an Ideal Mathematical Sandbox

At the heart of the art of mathematics lie Conjectures and Theorems. They are like the great novels and poems from Language Arts, students must know of them, not merely because of the skills they develop that have real world application, but also because they are part of a beautiful tapestry of the development of mathematics.

A modern day unsolved problem in mathematics involves a conjecture that has stumped mathematicians for over 80 years. You may have heard of Collatz Conjecture, as it recently has gotten some press due to Terence Tao working on the problem, and surprisingly making some progress! Yet, it’s simple enough to explore with a 2nd grader or maybe younger.

Paul Erdos famously referred to it when he said:

"Mathematics is not yet ready for such problems."

I like exposing students to unsolved problems in mathematics, because it gives them a real sense for what mathematicians do. It takes pressure off of finding a “final solution” and shifts the focus towards exploring patterns and structure.

As a teacher, I have explored Collatz Conjecture with a variety of ages. I wanted to share one of my most fruitful experiences exploring the conjecture with a multigrade class of 5th and 6th graders (However, this can easily be adapted for younger or older students)..

Below you will find a game I use to introduce the conjecture, and a project I designed for the students to explore a method for reversing the recursive formula in order to "grow the Collatz tree" and look deeper into the patterns and structure.

This investigation aligns particularly nicely with a few of the Expressions and Equations standards, such as 6.EE.A.1-2, and 6.EE.B.5, along with all 8 Mathematical Practices!

Collatz Conjecture:

1. Take any natural number n.

2. If it’s even, divide by two, if it’s odd, multiply by three and add one.

Repeat step 2 indefinitely. The conjecture states that you will always reach the number one eventually.

For example, say you start with 5 your sequence would go 5-16-8-4-2-1.

Collatz Game Intro

The primary way I've used to introduce Collatz Conjecture is to have the students play a game where they roll a 10 sided die for a starting number. Then the person who gets to one in the most number of steps wins. Students quickly realize (or I help guide them towards the idea) that they can create a diagram, or tree network, which tells them right away who will win. Sometimes we extend it, by playing the game with 20-sided die and trying to solve that version as well. Below is what a tree might look like when using 10-sided dice.

When playing with a 10-sided die, 9 is the best roll, as it is the farthest number of steps from 1.

Exploring the Collatz Tree: Notice and Wonder

After the game intro, I like to do a “Notice and Wonder” session with the students, where I write down their observations and questions that come up. This list always ends up including some variation on the question “does it always end up at one?”

At the end of the Notice/Wonder session I explain what Collatz Conjecture is, and give some historical and mathematical context to get students excited about it. For example, I let them know that a proof of the conjecture could potentially earn the author(s) an honorary PH.D, and certainly fame.

Letting Kids Wander in their Wonderings…

Over the years I have expanded on this portion of the project to allow students more time to explore the things they notice and wonder in small groups before jumping into making the poster with the Collatz Tree. I have given as much as 3 whole class periods to allow them to explore. Giving students a chance to dive down rabbit holes, hit walls, make lemmas (small conjectures), and prove or disprove their lemmas gives kids a true taste of what being a mathematician is like.

Growing the Collatz Tree by Reversing the Process…

Once students get familiar with the structure of the Collatz tree we talk a bit about what it would mean for the conjecture to be true. For example, could we prove that a certain set of numbers will always go to one? Quickly students discover that as soon as you hit a power of 2, you are dividing by two all the way down. I like calling this the "tower of powers" (because I’m a sucker for rhymes).

We use the powers of 2 as the "trunk" of our Collatz tree, and the first example of a way to “grow the Collatz Tree”. You can reverse the recursive formula and double any number to "grow a branch" of the tree. For example, 5 could have come from 10, which could have come from 20, which could have come from 40, etc.

Branching Rule (n-1)/3

Then I ask the students to notice when are there "branchings" in the tree, in other words when are there two numbers that will lead to the same number such as 5 and 32, both lead to 16. Here students have to think about when (x-1)/3 will have an integer solution. This happens when a number is one more than a multiple of three. We review the divisibility rule for 3, and try it out on a few examples.

Collatz Tree Posters

Students work in groups to apply these two methods to grow the Collatz tree. There are lots of opportunities to differentiate the process, as students notice patterns in branchings and some even write algebraic expressions to describe the branches. For example, the 3-6-12... branch above can be described as 3*2^n.

Here a couple examples from one of the first times I did the project:

Integrate Coding/CS

Coding is also something that naturally made its way into the project. Students have written a variety of programs in Scratch, python, etc. This project provides an authentic application for coding that allows students to explore the conjecture at more depth. The coding skills required are also quite accessible for middle school students.

Here’s a couple examples where students chose to include some coding into their exploration and poster making:

Extensions and Connections

1. If you extend the recursive formula into the complex plane you get the fractal below. For a thorough explanation check out the blog post by Nathaniel Johnston.

2^n

2. Dan Finkel over at mathforlove.com has a variation called "The Dr Squares Puzzle" where they come up with a similar recursive process, with a few loops.

3. Here's another recursive process involving numbers and their written form (It also has a tree structure):

Step one: choose a natural number N

Step two: write the number in words, count the number of letters in the word and write that number.

Step 3: Repeat Step two.

For example: One-3-Three-5-Five-4-Four... stays at four indefinitely. You can also try other languages. :)

Finally, a post on Collatz Conjecture wouldn't be complete without this from XKCD: