At the heart of the art of mathematics lie Conjectures and Theorems. They are like the great novels and poems from Language Arts, students must know of them, not merely because of the skills they develop that have real world application, but also because they are part of a beautiful tapestry of the development of mathematics.
A modern day unsolved problem in mathematics involves a conjecture that has stumped mathematicians for over 80 years. You may have heard of Collatz Conjecture, as it recently has gotten some press due to Terence Tao working on the problem, and surprisingly making some progress! Yet, it’s simple enough to explore with a 2nd grader or maybe younger.
Paul Erdos famously referred to it when he said:
"Mathematics is not yet ready for such problems."
I like exposing students to unsolved problems in mathematics, because it gives them a real sense for what mathematicians do. It takes pressure off of finding a “final solution” and shifts the focus towards exploring patterns and structure.
As a teacher, I have explored Collatz Conjecture with a variety of ages. I wanted to share one of my most fruitful experiences exploring the conjecture with a multigrade class of 5th and 6th graders (However, this can easily be adapted for younger or older students)..
Below you will find a game I use to introduce the conjecture, and a project I designed for the students to explore a method for reversing the recursive formula in order to "grow the Collatz tree" and look deeper into the patterns and structure.
This investigation aligns particularly nicely with a few of the Expressions and Equations standards, such as 6.EE.A.1-2, and 6.EE.B.5, along with all 8 Mathematical Practices!
Collatz Conjecture:
1. Take any natural number n.
2. If it’s even, divide by two, if it’s odd, multiply by three and add one.
Repeat step 2 indefinitely. The conjecture states that you will always reach the number one eventually.
For example, say you start with 5 your sequence would go 5-16-8-4-2-1.
Collatz Game Intro
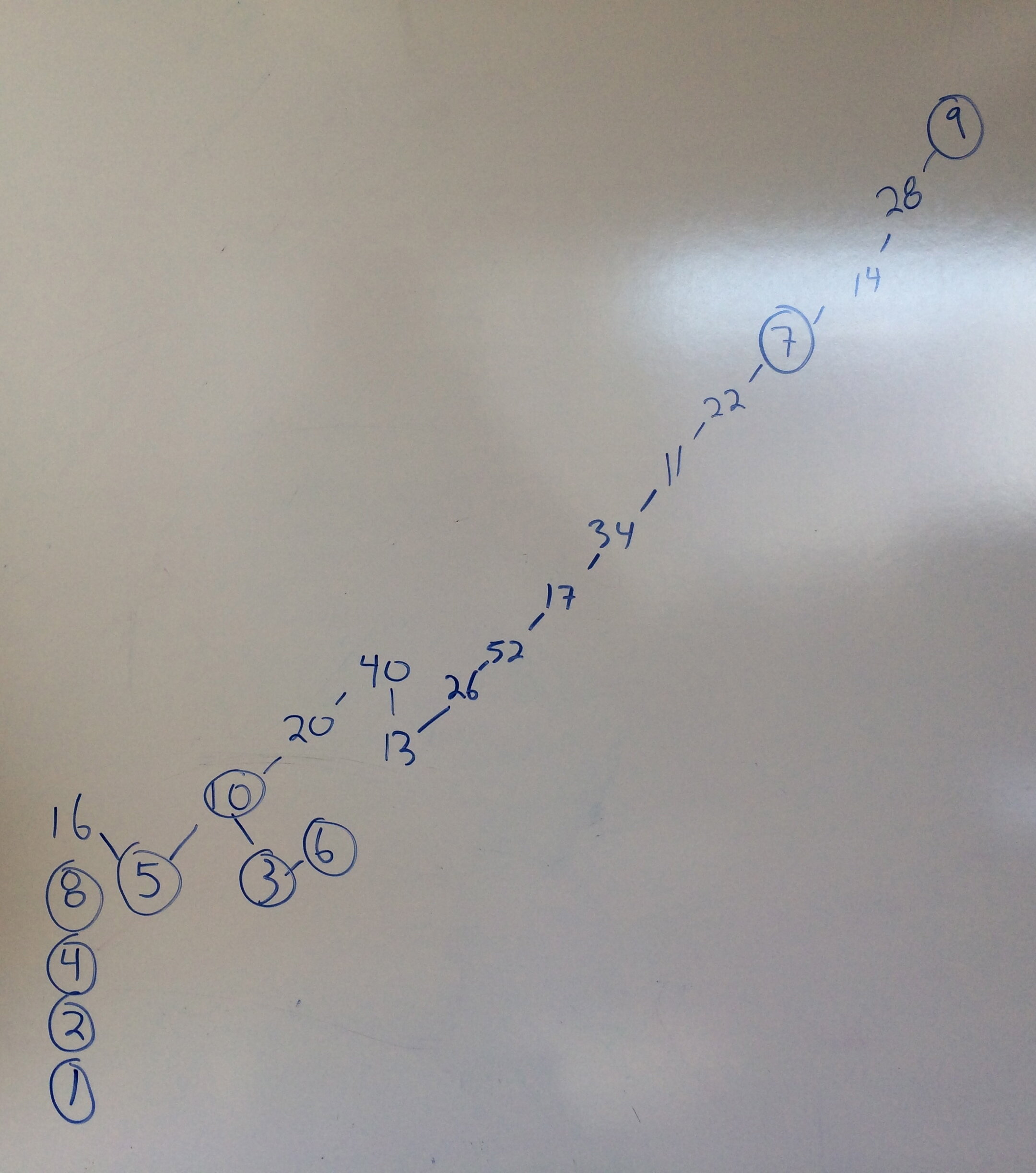
The primary way I've used to introduce Collatz Conjecture is to have the students play a game where they roll a 10 sided die for a starting number. Then the person who gets to one in the most number of steps wins. Students quickly realize (or I help guide them towards the idea) that they can create a diagram, or tree network, which tells them right away who will win. Sometimes we extend it, by playing the game with 20-sided die and trying to solve that version as well. Below is what a tree might look like when using 10-sided dice.
When playing with a 10-sided die, 9 is the best roll, as it is the farthest number of steps from 1.
Exploring the Collatz Tree: Notice and Wonder
After the game intro, I like to do a “Notice and Wonder” session with the students, where I write down their observations and questions that come up. This list always ends up including some variation on the question “does it always end up at one?”
At the end of the Notice/Wonder session I explain what Collatz Conjecture is, and give some historical and mathematical context to get students excited about it. For example, I let them know that a proof of the conjecture could potentially earn the author(s) an honorary PH.D, and certainly fame.
Letting Kids Wander in their Wonderings…
Over the years I have expanded on this portion of the project to allow students more time to explore the things they notice and wonder in small groups before jumping into making the poster with the Collatz Tree. I have given as much as 3 whole class periods to allow them to explore. Giving students a chance to dive down rabbit holes, hit walls, make lemmas (small conjectures), and prove or disprove their lemmas gives kids a true taste of what being a mathematician is like.
Growing the Collatz Tree by Reversing the Process…
Once students get familiar with the structure of the Collatz tree we talk a bit about what it would mean for the conjecture to be true. For example, could we prove that a certain set of numbers will always go to one? Quickly students discover that as soon as you hit a power of 2, you are dividing by two all the way down. I like calling this the "tower of powers" (because I’m a sucker for rhymes).
We use the powers of 2 as the "trunk" of our Collatz tree, and the first example of a way to “grow the Collatz Tree”. You can reverse the recursive formula and double any number to "grow a branch" of the tree. For example, 5 could have come from 10, which could have come from 20, which could have come from 40, etc.
Branching Rule (n-1)/3
Then I ask the students to notice when are there "branchings" in the tree, in other words when are there two numbers that will lead to the same number such as 5 and 32, both lead to 16. Here students have to think about when (x-1)/3 will have an integer solution. This happens when a number is one more than a multiple of three. We review the divisibility rule for 3, and try it out on a few examples.
Collatz Tree Posters
Students work in groups to apply these two methods to grow the Collatz tree. There are lots of opportunities to differentiate the process, as students notice patterns in branchings and some even write algebraic expressions to describe the branches. For example, the 3-6-12... branch above can be described as 3*2^n.
Here a couple examples from one of the first times I did the project:
Integrate Coding/CS
Coding is also something that naturally made its way into the project. Students have written a variety of programs in Scratch, python, etc. This project provides an authentic application for coding that allows students to explore the conjecture at more depth. The coding skills required are also quite accessible for middle school students.
Here’s a couple examples where students chose to include some coding into their exploration and poster making:
Extensions and Connections
1. If you extend the recursive formula into the complex plane you get the fractal below. For a thorough explanation check out the blog post by Nathaniel Johnston.
2^n
2. Dan Finkel over at mathforlove.com has a variation called "The Dr Squares Puzzle" where they come up with a similar recursive process, with a few loops.
3. Here's another recursive process involving numbers and their written form (It also has a tree structure):
Step one: choose a natural number N
Step two: write the number in words, count the number of letters in the word and write that number.
Step 3: Repeat Step two.
For example: One-3-Three-5-Five-4-Four... stays at four indefinitely. You can also try other languages. :)
Finally, a post on Collatz Conjecture wouldn't be complete without this from XKCD: